Frekvenční vs Bayesovská statistika. Jak subjektivní názor ovlivňuje pravděpodobnost jevu?
„Nevěřím žádné statistice, kterou jsem sám nezfalšoval.“ - Winston Churchill
Statistika
Analytika
2. 3. 2024





V článku se dozvíte:
Frekvenční (klasická) statistika
Bayesovská inference
Bayesovský přístup
Podmíněna pravděpodobnost
Zobecnění Bayesová vzorce na data
Frekvenční (klasická) statistika
Frekvenční statistika je nejrozšířenějším a nejvíce populárním způsobem statistického usuzování, jehož dominance plyne zejména z jejího významného rozvoje v průběhu dvacátého století. Téměř veškerá statistická inference (usuzování o populaci na základě vzorce) používaná dnes (např. v sociálních vědách) je založená na klasickém pojetí statistiky. Zákon velkých čísel, který spadá do klasické statistiky, říká, že relativní četnost velkého počtu nezávislých náhodných pokusů se při opakování se přibližuje k jednomu číslu/relativní četnosti (skutečné pravděpodobnosti daného jevu). Vzhledem k této definici se u frekvenční statistiky předpokládá, že data jsou získaná náhodným výběrem a jen na základě takových dat je možné provádět zobecňující úsudky o celé populaci.
Frekvenční statistika při výpočtech vychází z tzv. výběrového rozdělení, což je pro ne-statistiky docela komplikovaný pojem. Je důležité chápat rozdíl mezi pojmy "výběrové rozdělení" a "rozdělení výběru". Sample distribution (rozdělení výběru) - je rozdělením dat z jednoho výběru. Sampling distribution (rozdělení výběrů) – rozdělení všech možných výběrů z populace (teoretický koncept).
Bayesovská inference
Bayesovská inference umožňuje za použití nějaké naší původní představy o hodnotě parametru/zkušeností/znalostí (apriorní informace) a na základě informací z provedeného výběru (tedy získaných dat), určit hodnotu tohoto parametru pomocí posteriorního rozdělení (viz. dále).
Bayesovský přístup
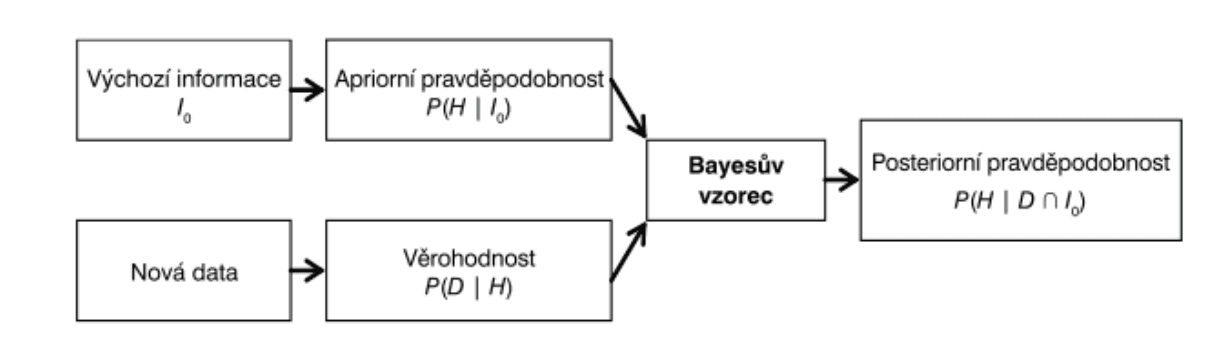
Bayesovský přístup při odhadech, usuzování a vytváření modelů lze specifikovat pomocí následujících kroků:
Na základě výchozí informace specifikujeme apriorní rozdělení pro parametr modelu. Apriorní rozdělní P(H|I_o) lze interpretovat jako pravděpodobnost parametru modelu za podmínky výchozí informace (subjektivního názoru/znalostí/zkušeností/získané externí informace);
Na základě získaných dat vytvoříme věrohodnostní funkci, která představuje pravděpodobnost získaných dat za podminky, že parametr nabývá hodnoty H -> P(D|H) , kde D - získaná data;
Pomocí Bayesova vzorce z apriorního rozdělení a věrohodnostní funkce získáme posteriorní rozdělení pro parametry modelu. Posteriorní rozdělení říká, jaká je pravděpodobnost paramentru za podmínky, že máme získaná data D a výchozí informace (subjektivní názor) I_o→ P(H│D∩I_o), kde znak ∩ znamená průnik dvou jevů (dva jevy nastanou současně). Posteriorní rozdělení se také interpretuje jako míra důvěry v nastoupení daného jevu;
Pomocí simulačních technik pak získáme výběr z posteriorního rozdělení a odhadneme parametr (v klasické statistice se nikdy neodhadují parametry pomocí simulace. Pouze na základě získaných dat).
Podmíněná pravděpodobnost
Představa podmíněnosti je nezbytná pro bayesovské usuzování.
Podmíněná pravděpodobnost znamená, že pravděpodobnost výskytu určitého jevu závisí na tom, zda nastal, nebo nenastal nějaký jiný jev. Podmíněné pravděpodobnosti se značí P(A│B), což čteme jako pravděpodobnost jevu A za předpokladu, že nastal jev B. Pro podmíněné pravděpodobnosti platí všechna základní pravidla pravděpodobnosti. Při úvahách o podmíněné pravděpodobnosti se často používá Bayesova věta (Hendl, 2012, s. 126).
Zobecnění Bayesová vzorce na data
Jiné odvození Bayesova vzorce je založené na tom, že sdružená pravděpodobnost dvou jevů (pravděpodobnost průniku dvou jevů; označme je nyní jako jev P a jev D) může být zapsána jako součin pravděpodobnosti jednoho z jevů a podmíněné pravděpodobnosti druhého jevu, za předpokladu prvního jevu.
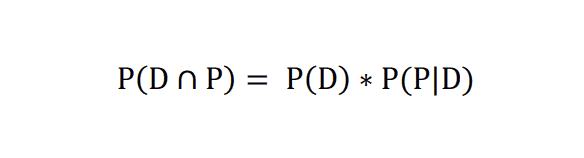
Při prohození dvou jevů může být pravděpodobnost zapsána také jako:
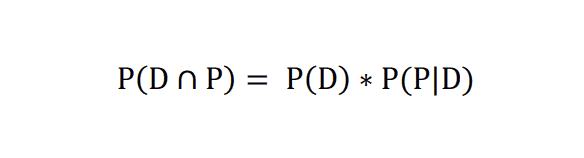
Protože levé strany jsou si rovny, pak platí rovnost i pro obě pravé strany. Když je dáme do rovnosti a upravíme, pak dostaneme:
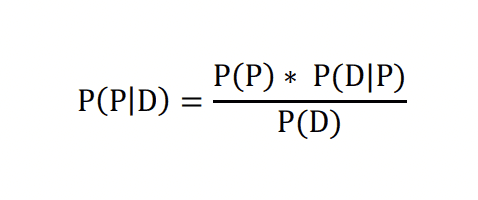
Zjednodušená Bayesova věta se uvádí s vynecháním P(D), což je prediktivní pravděpodobnost vyplývající z věrohodností a apriorních pravděpodobností (Hebák, 2012a, s. 84). Vynechává se proto, že může být někdy těžce spočitatelná a nemění relativní pravděpodobnost parametru. Zjednodušená Bayesova věta tedy vypadá jako:
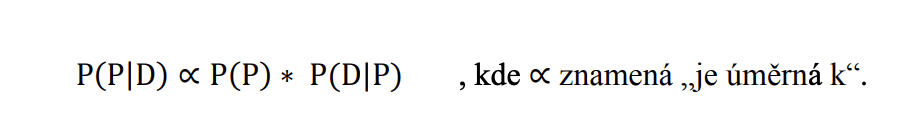
Nyní si můžeme představit, že jev P představuje parametr (hypotézu nebo model) a jev D představuje data. Levá strana Bayesovy věty P(P|D) pak odpovídá posteriorní pravděpodobnosti neboli pravděpodobnost parametru P, za předpokladu napozorovaných dat D.
Na pravé straně je pravděpodobnost P(P), tedy apriorní pravděpodobnost přidělená parametru před tím, než nám jsou data známa (subjektivní názor). Pravděpodobnost P(D|P) je výběrová hustota dat (sampling density of the data), která je proporcionální věrohodnosti neboli informaci poskytnuté daty (Western, 1999, s. 13).
Slovně tedy můžeme Bayesovu větu vyjádřit jako: Posteriorní rozdělení = apriorní rozdělení * věrohodnostní funkce.
Frekvenční (klasická) statistika
Frekvenční statistika je nejrozšířenějším a nejvíce populárním způsobem statistického usuzování, jehož dominance plyne zejména z jejího významného rozvoje v průběhu dvacátého století. Téměř veškerá statistická inference (usuzování o populaci na základě vzorce) používaná dnes (např. v sociálních vědách) je založená na klasickém pojetí statistiky. Zákon velkých čísel, který spadá do klasické statistiky, říká, že relativní četnost velkého počtu nezávislých náhodných pokusů se při opakování se přibližuje k jednomu číslu/relativní četnosti (skutečné pravděpodobnosti daného jevu). Vzhledem k této definici se u frekvenční statistiky předpokládá, že data jsou získaná náhodným výběrem a jen na základě takových dat je možné provádět zobecňující úsudky o celé populaci.
Frekvenční statistika při výpočtech vychází z tzv. výběrového rozdělení, což je pro ne-statistiky docela komplikovaný pojem. Je důležité chápat rozdíl mezi pojmy "výběrové rozdělení" a "rozdělení výběru". Sample distribution (rozdělení výběru) - je rozdělením dat z jednoho výběru. Sampling distribution (rozdělení výběrů) – rozdělení všech možných výběrů z populace (teoretický koncept).
Bayesovská inference
Bayesovská inference umožňuje za použití nějaké naší původní představy o hodnotě parametru/zkušeností/znalostí (apriorní informace) a na základě informací z provedeného výběru (tedy získaných dat), určit hodnotu tohoto parametru pomocí posteriorního rozdělení (viz. dále).
Bayesovský přístup
Bayesovský přístup při odhadech, usuzování a vytváření modelů lze specifikovat pomocí následujících kroků:
Na základě výchozí informace specifikujeme apriorní rozdělení pro parametr modelu. Apriorní rozdělní P(H|I_o) lze interpretovat jako pravděpodobnost parametru modelu za podmínky výchozí informace (subjektivního názoru/znalostí/zkušeností/získané externí informace);
Na základě získaných dat vytvoříme věrohodnostní funkci, která představuje pravděpodobnost získaných dat za podminky, že parametr nabývá hodnoty H -> P(D|H) , kde D - získaná data;
Pomocí Bayesova vzorce z apriorního rozdělení a věrohodnostní funkce získáme posteriorní rozdělení pro parametry modelu. Posteriorní rozdělení říká, jaká je pravděpodobnost paramentru za podmínky, že máme získaná data D a výchozí informace (subjektivní názor) I_o→ P(H│D∩I_o), kde znak ∩ znamená průnik dvou jevů (dva jevy nastanou současně). Posteriorní rozdělení se také interpretuje jako míra důvěry v nastoupení daného jevu;
Pomocí simulačních technik pak získáme výběr z posteriorního rozdělení a odhadneme parametr (v klasické statistice se nikdy neodhadují parametry pomocí simulace. Pouze na základě získaných dat).

Podmíněná pravděpodobnost
Představa podmíněnosti je nezbytná pro bayesovské usuzování.
Podmíněná pravděpodobnost znamená, že pravděpodobnost výskytu určitého jevu závisí na tom, zda nastal, nebo nenastal nějaký jiný jev. Podmíněné pravděpodobnosti se značí P(A│B), což čteme jako pravděpodobnost jevu A za předpokladu, že nastal jev B. Pro podmíněné pravděpodobnosti platí všechna základní pravidla pravděpodobnosti. Při úvahách o podmíněné pravděpodobnosti se často používá Bayesova věta (Hendl, 2012, s. 126).
Zobecnění Bayesová vzorce na data
Jiné odvození Bayesova vzorce je založené na tom, že sdružená pravděpodobnost dvou jevů (pravděpodobnost průniku dvou jevů; označme je nyní jako jev P a jev D) může být zapsána jako součin pravděpodobnosti jednoho z jevů a podmíněné pravděpodobnosti druhého jevu, za předpokladu prvního jevu.
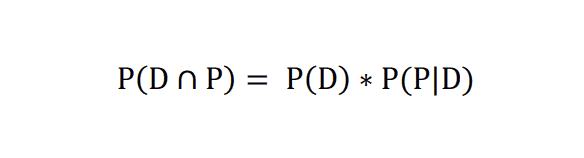
Při prohození dvou jevů může být pravděpodobnost zapsána také jako:
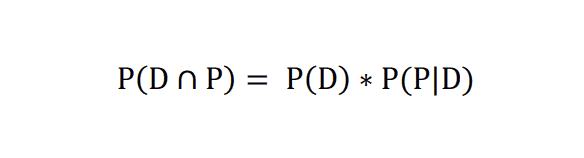
Protože levé strany jsou si rovny, pak platí rovnost i pro obě pravé strany. Když je dáme do rovnosti a upravíme, pak dostaneme:
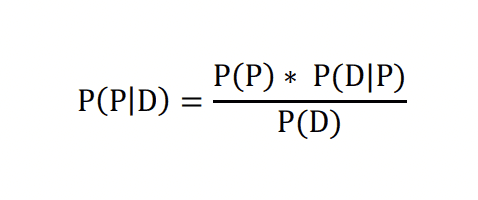
Zjednodušená Bayesova věta se uvádí s vynecháním P(D), což je prediktivní pravděpodobnost vyplývající z věrohodností a apriorních pravděpodobností (Hebák, 2012a, s. 84). Vynechává se proto, že může být někdy těžce spočitatelná a nemění relativní pravděpodobnost parametru. Zjednodušená Bayesova věta tedy vypadá jako:
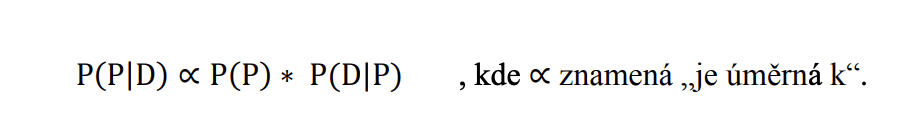
Nyní si můžeme představit, že jev P představuje parametr (hypotézu nebo model) a jev D představuje data. Levá strana Bayesovy věty P(P|D) pak odpovídá posteriorní pravděpodobnosti neboli pravděpodobnost parametru P, za předpokladu napozorovaných dat D.
Na pravé straně je pravděpodobnost P(P), tedy apriorní pravděpodobnost přidělená parametru před tím, než nám jsou data známa (subjektivní názor). Pravděpodobnost P(D|P) je výběrová hustota dat (sampling density of the data), která je proporcionální věrohodnosti neboli informaci poskytnuté daty (Western, 1999, s. 13).
Slovně tedy můžeme Bayesovu větu vyjádřit jako: Posteriorní rozdělení = apriorní rozdělení * věrohodnostní funkce.
Frekvenční (klasická) statistika
Frekvenční statistika je nejrozšířenějším a nejvíce populárním způsobem statistického usuzování, jehož dominance plyne zejména z jejího významného rozvoje v průběhu dvacátého století. Téměř veškerá statistická inference (usuzování o populaci na základě vzorce) používaná dnes (např. v sociálních vědách) je založená na klasickém pojetí statistiky. Zákon velkých čísel, který spadá do klasické statistiky, říká, že relativní četnost velkého počtu nezávislých náhodných pokusů se při opakování se přibližuje k jednomu číslu/relativní četnosti (skutečné pravděpodobnosti daného jevu). Vzhledem k této definici se u frekvenční statistiky předpokládá, že data jsou získaná náhodným výběrem a jen na základě takových dat je možné provádět zobecňující úsudky o celé populaci.
Frekvenční statistika při výpočtech vychází z tzv. výběrového rozdělení, což je pro ne-statistiky docela komplikovaný pojem. Je důležité chápat rozdíl mezi pojmy "výběrové rozdělení" a "rozdělení výběru". Sample distribution (rozdělení výběru) - je rozdělením dat z jednoho výběru. Sampling distribution (rozdělení výběrů) – rozdělení všech možných výběrů z populace (teoretický koncept).
Bayesovská inference
Bayesovská inference umožňuje za použití nějaké naší původní představy o hodnotě parametru/zkušeností/znalostí (apriorní informace) a na základě informací z provedeného výběru (tedy získaných dat), určit hodnotu tohoto parametru pomocí posteriorního rozdělení (viz. dále).
Bayesovský přístup
Bayesovský přístup při odhadech, usuzování a vytváření modelů lze specifikovat pomocí následujících kroků:
Na základě výchozí informace specifikujeme apriorní rozdělení pro parametr modelu. Apriorní rozdělní P(H|I_o) lze interpretovat jako pravděpodobnost parametru modelu za podmínky výchozí informace (subjektivního názoru/znalostí/zkušeností/získané externí informace);
Na základě získaných dat vytvoříme věrohodnostní funkci, která představuje pravděpodobnost získaných dat za podminky, že parametr nabývá hodnoty H -> P(D|H) , kde D - získaná data;
Pomocí Bayesova vzorce z apriorního rozdělení a věrohodnostní funkce získáme posteriorní rozdělení pro parametry modelu. Posteriorní rozdělení říká, jaká je pravděpodobnost paramentru za podmínky, že máme získaná data D a výchozí informace (subjektivní názor) I_o→ P(H│D∩I_o), kde znak ∩ znamená průnik dvou jevů (dva jevy nastanou současně). Posteriorní rozdělení se také interpretuje jako míra důvěry v nastoupení daného jevu;
Pomocí simulačních technik pak získáme výběr z posteriorního rozdělení a odhadneme parametr (v klasické statistice se nikdy neodhadují parametry pomocí simulace. Pouze na základě získaných dat).

Podmíněná pravděpodobnost
Představa podmíněnosti je nezbytná pro bayesovské usuzování.
Podmíněná pravděpodobnost znamená, že pravděpodobnost výskytu určitého jevu závisí na tom, zda nastal, nebo nenastal nějaký jiný jev. Podmíněné pravděpodobnosti se značí P(A│B), což čteme jako pravděpodobnost jevu A za předpokladu, že nastal jev B. Pro podmíněné pravděpodobnosti platí všechna základní pravidla pravděpodobnosti. Při úvahách o podmíněné pravděpodobnosti se často používá Bayesova věta (Hendl, 2012, s. 126).
Zobecnění Bayesová vzorce na data
Jiné odvození Bayesova vzorce je založené na tom, že sdružená pravděpodobnost dvou jevů (pravděpodobnost průniku dvou jevů; označme je nyní jako jev P a jev D) může být zapsána jako součin pravděpodobnosti jednoho z jevů a podmíněné pravděpodobnosti druhého jevu, za předpokladu prvního jevu.
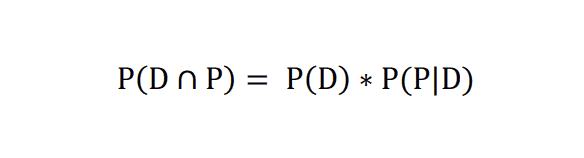
Při prohození dvou jevů může být pravděpodobnost zapsána také jako:
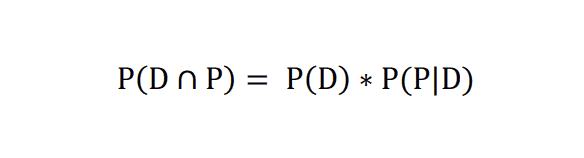
Protože levé strany jsou si rovny, pak platí rovnost i pro obě pravé strany. Když je dáme do rovnosti a upravíme, pak dostaneme:
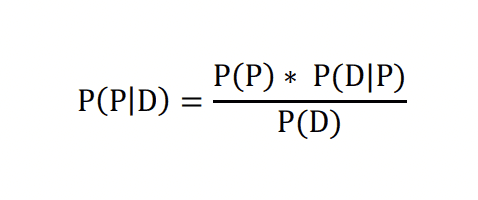
Zjednodušená Bayesova věta se uvádí s vynecháním P(D), což je prediktivní pravděpodobnost vyplývající z věrohodností a apriorních pravděpodobností (Hebák, 2012a, s. 84). Vynechává se proto, že může být někdy těžce spočitatelná a nemění relativní pravděpodobnost parametru. Zjednodušená Bayesova věta tedy vypadá jako:
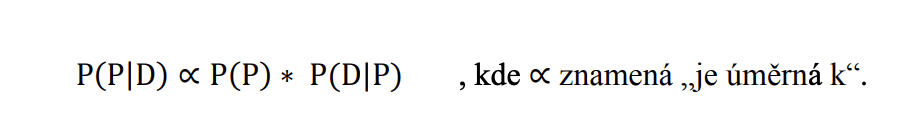
Nyní si můžeme představit, že jev P představuje parametr (hypotézu nebo model) a jev D představuje data. Levá strana Bayesovy věty P(P|D) pak odpovídá posteriorní pravděpodobnosti neboli pravděpodobnost parametru P, za předpokladu napozorovaných dat D.
Na pravé straně je pravděpodobnost P(P), tedy apriorní pravděpodobnost přidělená parametru před tím, než nám jsou data známa (subjektivní názor). Pravděpodobnost P(D|P) je výběrová hustota dat (sampling density of the data), která je proporcionální věrohodnosti neboli informaci poskytnuté daty (Western, 1999, s. 13).
Slovně tedy můžeme Bayesovu větu vyjádřit jako: Posteriorní rozdělení = apriorní rozdělení * věrohodnostní funkce.
Frekvenční (klasická) statistika
Frekvenční statistika je nejrozšířenějším a nejvíce populárním způsobem statistického usuzování, jehož dominance plyne zejména z jejího významného rozvoje v průběhu dvacátého století. Téměř veškerá statistická inference (usuzování o populaci na základě vzorce) používaná dnes (např. v sociálních vědách) je založená na klasickém pojetí statistiky. Zákon velkých čísel, který spadá do klasické statistiky, říká, že relativní četnost velkého počtu nezávislých náhodných pokusů se při opakování se přibližuje k jednomu číslu/relativní četnosti (skutečné pravděpodobnosti daného jevu). Vzhledem k této definici se u frekvenční statistiky předpokládá, že data jsou získaná náhodným výběrem a jen na základě takových dat je možné provádět zobecňující úsudky o celé populaci.
Frekvenční statistika při výpočtech vychází z tzv. výběrového rozdělení, což je pro ne-statistiky docela komplikovaný pojem. Je důležité chápat rozdíl mezi pojmy "výběrové rozdělení" a "rozdělení výběru". Sample distribution (rozdělení výběru) - je rozdělením dat z jednoho výběru. Sampling distribution (rozdělení výběrů) – rozdělení všech možných výběrů z populace (teoretický koncept).
Bayesovská inference
Bayesovská inference umožňuje za použití nějaké naší původní představy o hodnotě parametru/zkušeností/znalostí (apriorní informace) a na základě informací z provedeného výběru (tedy získaných dat), určit hodnotu tohoto parametru pomocí posteriorního rozdělení (viz. dále).
Bayesovský přístup
Bayesovský přístup při odhadech, usuzování a vytváření modelů lze specifikovat pomocí následujících kroků:
Na základě výchozí informace specifikujeme apriorní rozdělení pro parametr modelu. Apriorní rozdělní P(H|I_o) lze interpretovat jako pravděpodobnost parametru modelu za podmínky výchozí informace (subjektivního názoru/znalostí/zkušeností/získané externí informace);
Na základě získaných dat vytvoříme věrohodnostní funkci, která představuje pravděpodobnost získaných dat za podminky, že parametr nabývá hodnoty H -> P(D|H) , kde D - získaná data;
Pomocí Bayesova vzorce z apriorního rozdělení a věrohodnostní funkce získáme posteriorní rozdělení pro parametry modelu. Posteriorní rozdělení říká, jaká je pravděpodobnost paramentru za podmínky, že máme získaná data D a výchozí informace (subjektivní názor) I_o→ P(H│D∩I_o), kde znak ∩ znamená průnik dvou jevů (dva jevy nastanou současně). Posteriorní rozdělení se také interpretuje jako míra důvěry v nastoupení daného jevu;
Pomocí simulačních technik pak získáme výběr z posteriorního rozdělení a odhadneme parametr (v klasické statistice se nikdy neodhadují parametry pomocí simulace. Pouze na základě získaných dat).

Podmíněná pravděpodobnost
Představa podmíněnosti je nezbytná pro bayesovské usuzování.
Podmíněná pravděpodobnost znamená, že pravděpodobnost výskytu určitého jevu závisí na tom, zda nastal, nebo nenastal nějaký jiný jev. Podmíněné pravděpodobnosti se značí P(A│B), což čteme jako pravděpodobnost jevu A za předpokladu, že nastal jev B. Pro podmíněné pravděpodobnosti platí všechna základní pravidla pravděpodobnosti. Při úvahách o podmíněné pravděpodobnosti se často používá Bayesova věta (Hendl, 2012, s. 126).
Zobecnění Bayesová vzorce na data
Jiné odvození Bayesova vzorce je založené na tom, že sdružená pravděpodobnost dvou jevů (pravděpodobnost průniku dvou jevů; označme je nyní jako jev P a jev D) může být zapsána jako součin pravděpodobnosti jednoho z jevů a podmíněné pravděpodobnosti druhého jevu, za předpokladu prvního jevu.
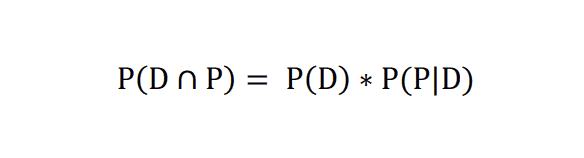
Při prohození dvou jevů může být pravděpodobnost zapsána také jako:
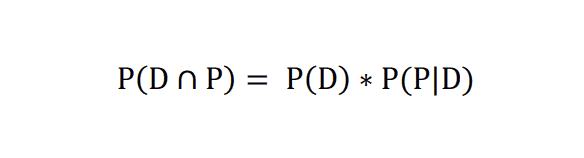
Protože levé strany jsou si rovny, pak platí rovnost i pro obě pravé strany. Když je dáme do rovnosti a upravíme, pak dostaneme:
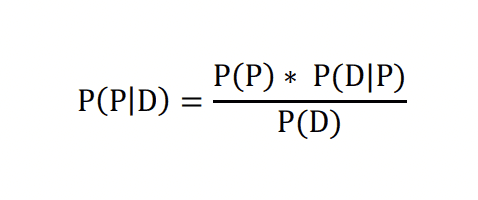
Zjednodušená Bayesova věta se uvádí s vynecháním P(D), což je prediktivní pravděpodobnost vyplývající z věrohodností a apriorních pravděpodobností (Hebák, 2012a, s. 84). Vynechává se proto, že může být někdy těžce spočitatelná a nemění relativní pravděpodobnost parametru. Zjednodušená Bayesova věta tedy vypadá jako:
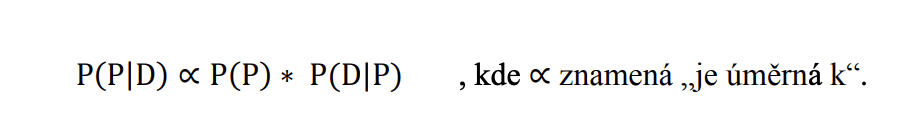
Nyní si můžeme představit, že jev P představuje parametr (hypotézu nebo model) a jev D představuje data. Levá strana Bayesovy věty P(P|D) pak odpovídá posteriorní pravděpodobnosti neboli pravděpodobnost parametru P, za předpokladu napozorovaných dat D.
Na pravé straně je pravděpodobnost P(P), tedy apriorní pravděpodobnost přidělená parametru před tím, než nám jsou data známa (subjektivní názor). Pravděpodobnost P(D|P) je výběrová hustota dat (sampling density of the data), která je proporcionální věrohodnosti neboli informaci poskytnuté daty (Western, 1999, s. 13).
Slovně tedy můžeme Bayesovu větu vyjádřit jako: Posteriorní rozdělení = apriorní rozdělení * věrohodnostní funkce.
Frekvenční (klasická) statistika
Frekvenční statistika je nejrozšířenějším a nejvíce populárním způsobem statistického usuzování, jehož dominance plyne zejména z jejího významného rozvoje v průběhu dvacátého století. Téměř veškerá statistická inference (usuzování o populaci na základě vzorce) používaná dnes (např. v sociálních vědách) je založená na klasickém pojetí statistiky. Zákon velkých čísel, který spadá do klasické statistiky, říká, že relativní četnost velkého počtu nezávislých náhodných pokusů se při opakování se přibližuje k jednomu číslu/relativní četnosti (skutečné pravděpodobnosti daného jevu). Vzhledem k této definici se u frekvenční statistiky předpokládá, že data jsou získaná náhodným výběrem a jen na základě takových dat je možné provádět zobecňující úsudky o celé populaci.
Frekvenční statistika při výpočtech vychází z tzv. výběrového rozdělení, což je pro ne-statistiky docela komplikovaný pojem. Je důležité chápat rozdíl mezi pojmy "výběrové rozdělení" a "rozdělení výběru". Sample distribution (rozdělení výběru) - je rozdělením dat z jednoho výběru. Sampling distribution (rozdělení výběrů) – rozdělení všech možných výběrů z populace (teoretický koncept).
Bayesovská inference
Bayesovská inference umožňuje za použití nějaké naší původní představy o hodnotě parametru/zkušeností/znalostí (apriorní informace) a na základě informací z provedeného výběru (tedy získaných dat), určit hodnotu tohoto parametru pomocí posteriorního rozdělení (viz. dále).
Bayesovský přístup
Bayesovský přístup při odhadech, usuzování a vytváření modelů lze specifikovat pomocí následujících kroků:
Na základě výchozí informace specifikujeme apriorní rozdělení pro parametr modelu. Apriorní rozdělní P(H|I_o) lze interpretovat jako pravděpodobnost parametru modelu za podmínky výchozí informace (subjektivního názoru/znalostí/zkušeností/získané externí informace);
Na základě získaných dat vytvoříme věrohodnostní funkci, která představuje pravděpodobnost získaných dat za podminky, že parametr nabývá hodnoty H -> P(D|H) , kde D - získaná data;
Pomocí Bayesova vzorce z apriorního rozdělení a věrohodnostní funkce získáme posteriorní rozdělení pro parametry modelu. Posteriorní rozdělení říká, jaká je pravděpodobnost paramentru za podmínky, že máme získaná data D a výchozí informace (subjektivní názor) I_o→ P(H│D∩I_o), kde znak ∩ znamená průnik dvou jevů (dva jevy nastanou současně). Posteriorní rozdělení se také interpretuje jako míra důvěry v nastoupení daného jevu;
Pomocí simulačních technik pak získáme výběr z posteriorního rozdělení a odhadneme parametr (v klasické statistice se nikdy neodhadují parametry pomocí simulace. Pouze na základě získaných dat).

Podmíněná pravděpodobnost
Představa podmíněnosti je nezbytná pro bayesovské usuzování.
Podmíněná pravděpodobnost znamená, že pravděpodobnost výskytu určitého jevu závisí na tom, zda nastal, nebo nenastal nějaký jiný jev. Podmíněné pravděpodobnosti se značí P(A│B), což čteme jako pravděpodobnost jevu A za předpokladu, že nastal jev B. Pro podmíněné pravděpodobnosti platí všechna základní pravidla pravděpodobnosti. Při úvahách o podmíněné pravděpodobnosti se často používá Bayesova věta (Hendl, 2012, s. 126).
Zobecnění Bayesová vzorce na data
Jiné odvození Bayesova vzorce je založené na tom, že sdružená pravděpodobnost dvou jevů (pravděpodobnost průniku dvou jevů; označme je nyní jako jev P a jev D) může být zapsána jako součin pravděpodobnosti jednoho z jevů a podmíněné pravděpodobnosti druhého jevu, za předpokladu prvního jevu.
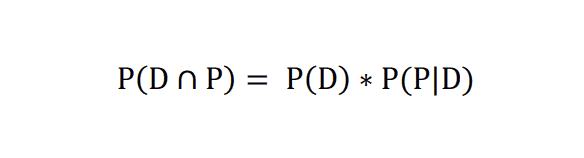
Při prohození dvou jevů může být pravděpodobnost zapsána také jako:
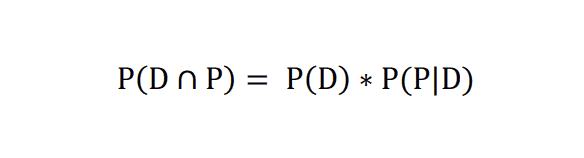
Protože levé strany jsou si rovny, pak platí rovnost i pro obě pravé strany. Když je dáme do rovnosti a upravíme, pak dostaneme:
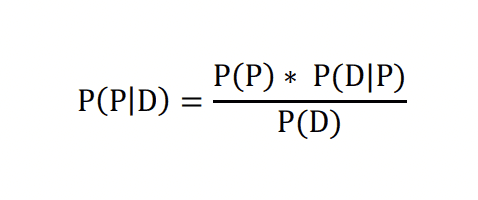
Zjednodušená Bayesova věta se uvádí s vynecháním P(D), což je prediktivní pravděpodobnost vyplývající z věrohodností a apriorních pravděpodobností (Hebák, 2012a, s. 84). Vynechává se proto, že může být někdy těžce spočitatelná a nemění relativní pravděpodobnost parametru. Zjednodušená Bayesova věta tedy vypadá jako:
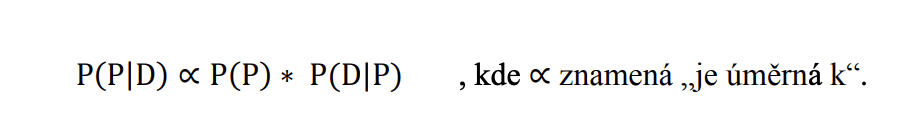
Nyní si můžeme představit, že jev P představuje parametr (hypotézu nebo model) a jev D představuje data. Levá strana Bayesovy věty P(P|D) pak odpovídá posteriorní pravděpodobnosti neboli pravděpodobnost parametru P, za předpokladu napozorovaných dat D.
Na pravé straně je pravděpodobnost P(P), tedy apriorní pravděpodobnost přidělená parametru před tím, než nám jsou data známa (subjektivní názor). Pravděpodobnost P(D|P) je výběrová hustota dat (sampling density of the data), která je proporcionální věrohodnosti neboli informaci poskytnuté daty (Western, 1999, s. 13).
Slovně tedy můžeme Bayesovu větu vyjádřit jako: Posteriorní rozdělení = apriorní rozdělení * věrohodnostní funkce.
CHCETE-LI PROBRAT VÁŠ PROJEKT NEBO ZÍSKAT VÍCE INFORMACÍ, KONTAKTUJTE MĚ:
CHCETE-LI PROBRAT VÁŠ PROJEKT NEBO ZÍSKAT VÍCE INFORMACÍ, KONTAKTUJTE MĚ:
CHCETE-LI PROBRAT VÁŠ PROJEKT NEBO ZÍSKAT VÍCE INFORMACÍ, KONTAKTUJTE MĚ:
CHCETE-LI PROBRAT VÁŠ PROJEKT NEBO ZÍSKAT VÍCE INFORMACÍ, KONTAKTUJTE MĚ:
CHCETE-LI PROBRAT VÁŠ PROJEKT NEBO ZÍSKAT VÍCE INFORMACÍ, KONTAKTUJTE MĚ: